This article requires a deliberate and careful series of hops across a path of conceptual steppingstones. So bring your light step and best leap and let’s get going on this journey that will take us across two very different worlds. To begin, I need to introduce you to an Indian mathematical genius called Srinivas Ramanujan who lived a tragically short 32 years from 1887 to 1920. What took him from a small Indian village to the pages of history was that despite a lack of formal training, he possessed an extremely rare level of mathematical intuition that enabled him to see patterns and solutions to complex problems that confounded the best minds. He is famous for his work on different kinds of infinite and hypergeometric series, branches of math that may not mean much to most of us. But this famous anecdote shared by his friend and fellow Mathematician GH Hardy of the University of Cambridge gives us a taste of his genius. Ramanujan was sick and in hospital one day, when he was visited by Hardy. Upon arrival Hardy made this rather strange observation to Ramanujan. He noted that the number of the taxicab he hailed to get to the hospital was 1729. He thought that it was a rather dull number and he hoped it was therefore not an unfavorable omen. To that Ramanujan instant replied, “no, it is a very interesting number. It is the smallest number that can be expressed as the sum of two cubes in two different ways”. 1729 happens to be both 13 +123 and 93 +103
The thing is, there are numerous and incredibly more complex and important relationships, patterns and properties within the world of numbers. To discover them, mathematicians work long and hard to propose a “conjecture” or a mathematician’s hypothesis. If it can be proved, the conjecture is elevated to the status as a “theorem”. Every now and then the world is gifted with those who might propose profound new conjectures or prove existing ones, which may one day go on to become the basis of great scientific progress. But because this is such a rarified field, it is not everyday that someone comes up with a new theorem that describes a new property within the world of numbers.
Until now that is. Because a group of Israeli computer scientists in the field of Artificial Intelligence have come up with an engine called the “Ramanujan Machine” that can spit out conjectures like a top-notch mathematician. Human mathematicians can then verify them to be true and put them on a shelf for any scientist to use in their own fields. So how does the Ramanujan Machine go about generating these remarkable conjectures? Well, the technique is most ingenious. The engine scans vast quantities of possible equations. While scanning, the machine is asked to look out for those equations that express the known “universal constants”. Universal constants are those numbers that express an important fundamental property of the universe. For example, consider the simplest such constant, π. π is simply the ratio of the circumference of a circle to its diameter. While the idea is simple enough, the number π cannot be written out as either a fraction or a decimal without approximating it. Yet, it is as much a part of the code that describes our universe as are circles. So, when scanning all possible equations that could exist, this machine is looking specifically for those equations that express these universal constants. The logic being that if the equation is expressing one or more of these universal constants which we already know to be universally true and of great significance, then such an equation will be of great value to our understanding of math itself and by extension the entire universe. This idea has been a triumph and many new mathematical ideas have already been discovered by the machine this way.
Why was this machine named after Srinivasan Ramanujan? Because unlike most mathematicians Ramanujan too spat out numerous fascinating mathematical ideas by starting with what he saw as a divine truth. In fact, he had made abundantly clear in his time that he saw value in an equation only if it expressed something about god.
What does this have to do with the Bible? This relationship between starting with a universal constant or universal truth and arriving at a helpful mathematical idea correlates strongly with a foundational Biblical axiom, “the fear of God is the beginning of wisdom”. What this verse is saying is that when a God who calls us to a deep reverential relationship with Himself is taken as the most fundamental given in our lives, then it enables us to access the best decision-making necessary to navigate the vicissitudes of life.
However, the very notion that there is such a fundamental given or “absolute truth” has in the time of postmodern relativism become anathema within our culture. The postmodern instinct is to dismiss all absolute givens or truths as a value of an older primitive era. The irony is that modern science is only possible because we have “universal” definitions and standards for every term and measure used by scientists. Today, all modern science is supported by an entire branch of the scientific endeavor whose sole purpose is to discover, measure, and provide references of these universal constants for the rest of the world of science and engineering. Further, the end of all scientific endeavor has always been to discover what is universally true of the structures of life, and the universe at every scale. A law that is true for one individual but not another, will be worth nothing in any scientific investigation.
Just as “universal constants” and “universal laws” enable us to assess the tremendous beauty and functionality of the mathematical and physical worlds, so also “universal truths” enable us to access all other spiritual and worldly truths. A special case of that is the previously referenced Biblical axiom, “the fear of God is the beginning of wisdom”.
It is a great tragedy that GH Hardy, the one credited for “discovering” Ramanujan was an atheist. It does not look like anybody was able to share the Gospel with our friend Ramanujan in his short earthly life. But I can see Jesus having this conversation with Ramanujan. “Ramanujan, from the deep well you have been given access to, can you offer me some truth that can satisfy my thirst?” “Sure, I don’t know who you are or why you want truth from me, but since you asked, may I offer you an infinite series that converges very quickly to the value of π?” Jesus on contemplating this equation responds, “That is elegant and insightful my friend. You are known as the man who knew infinity and for good reason. But if you knew who I was, it is you who would be asking me for the ‘universal truth’ that represents the only solution for a finite and fallen human to get to eternal life”.

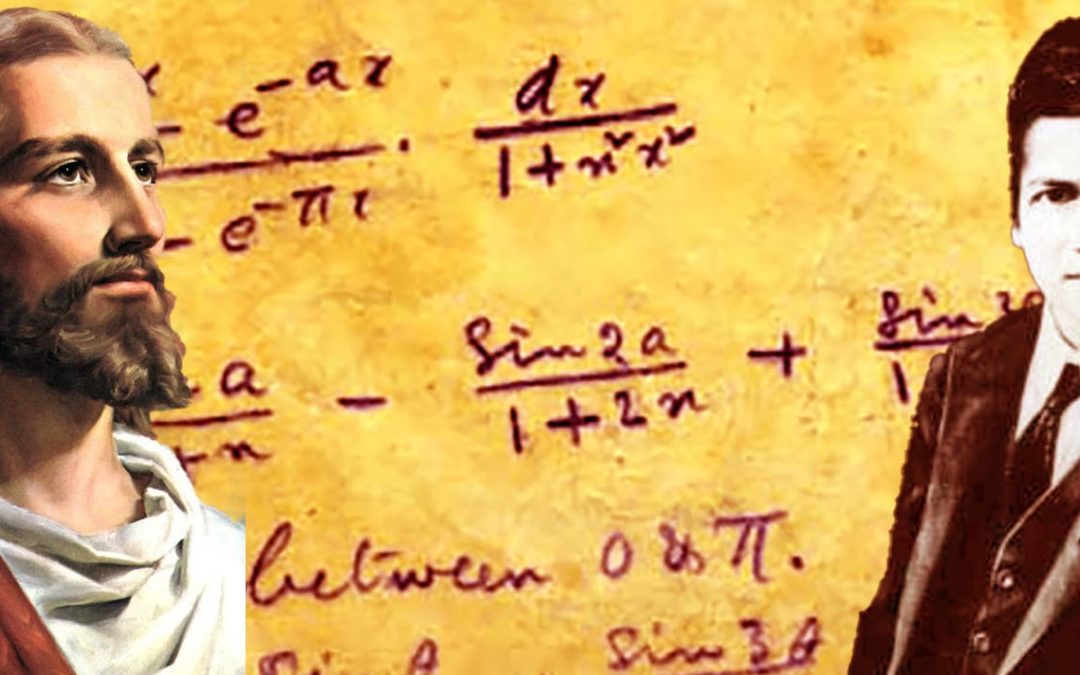
0 Comments